
Remember that an index in an array begins with 0. Using the above magic square as an example, we can say that number 2 is on row 0 column 0, and number 3 is on row 2 column 1. In other words, each cell in a 2D array is identified according to its row index and column index. Therefore, to refer to each cell in a 2D array, we need 2 indices, one for the row, and one for the column. Now, with a 2D array, we can have multiple collections of data, visualised as multiple rows of cells which are arranged close together, forming rows and columns. What is a 2-dimensional (2D) array? Well, in previous examples, we use a single row of connected boxes to visualise the concept of a one-dimensional array (which we simply call an array) to hold a collection of data. So here, we will use a 2-dimensional array as the container representing the matrix. In this example, we will read a series of 9 numbers and arrange them in a 3×3 matrix.

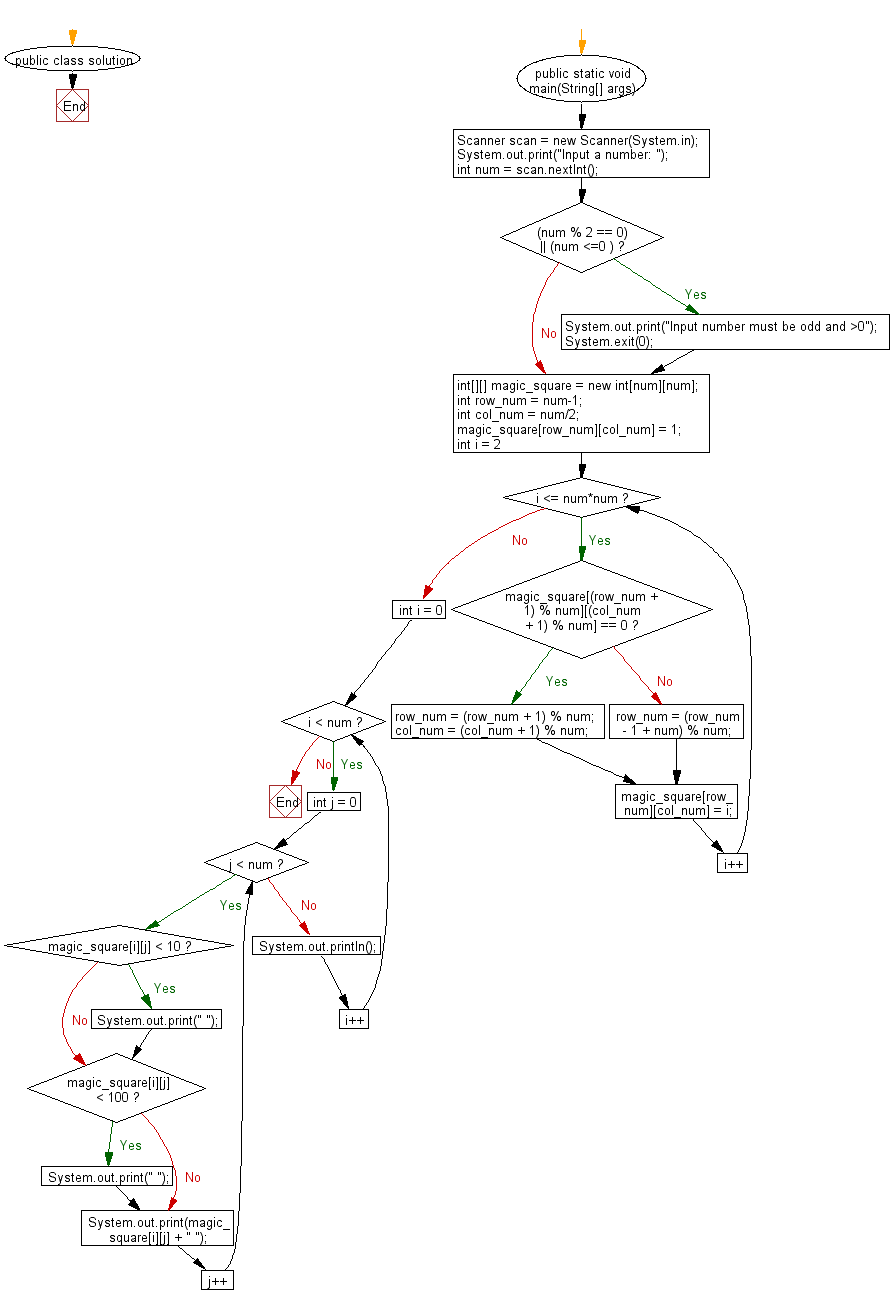
The program below shows how we can determine whether a series of 9 numbers forms a magic square or not. A magic square can be composed of 9 numbers (3 by 3 grid), 16 numbers (4 by 4), and so on, as long as they form a square, obviously! Not every square grid of numbers is a magic square, only when it satisfies this rule. If we sum up the numbers on each row, (2+7+6, 9+5+1, and 4+3+8) the results are the same, which is 15.

A magic square is an arrangement of unrepeated integer numbers in a square grid, where the sum of numbers in each row, column, and the main and secondary diagonals, all add up to the same number.


 0 kommentar(er)
0 kommentar(er)
